1. 前言
2. 简介和一些理解
3. 文字实现
4. 代码实现
5. 常用拓展
   1. 数学相关操作
   2. 最大子段和
   3. 区间数数
   4. 二维偏序
6. 常用扩展
   1. 动态开点线段树
   2. 标记永久化
   3. zkw 线段树
7. 关于树状数组

前言

我对于数据结构的喜爱可能是源于线段树, 庞大的代码量, 理清思路后只要背诵模板就能轻易过题, 题目描述清晰易懂, 模块化, 可复用, 这些数据结构题独有的特点都吸引了我

线段树其实很早之前我就把模板题过了, 但是半年多过去了, 做了几十道题目, 我还是不敢说自己完全掌握了线段树, 只是完成了树链剖分的笔记后, 觉得必须写一篇线段树来弥补基础数据结构的空缺, 于是就有了这篇文章

只有在不间断的, 大量的修改之中, 线段树才能体现出其优势; 我们也一样

简介和一些理解

线段树的单次修改 / 查询操作时间复杂度是的, 这得益于它将数据二分并存储的特点 ( 也是因此线段树需要 4 倍于数据的空间的原因, 因为它是一棵完全二叉树, 但严格来说, 其实是 )

线段树认为单个数据也是一个区间

线段树能维护的数据必须线性可分, 即, 将序列分为左右两个子序列, 分别计算, 得到的结果可以通过某种方式合并成整个序列的结果

结合上面两点, 线段树用类似归并排序的方式, 不断二分序列, 直到只剩一个元素, 然后再回溯, 在回溯过程中两两合并序列, 建成一棵分层的树, 每次执行操作就将目标区间分为若干线段树中区间的并 ( 形式化地, 令为目标区间, 为划分出的区间, 则, 且 ), 这是线段树的核心思想

文字实现

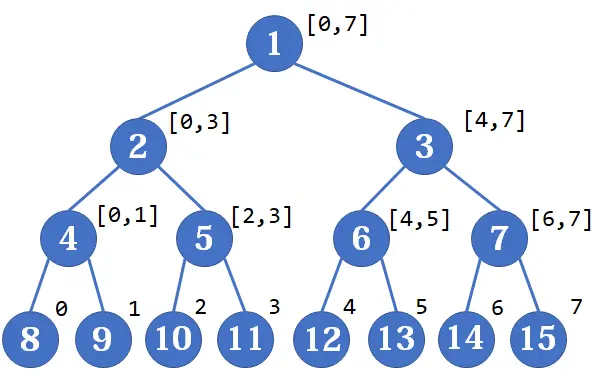
观察线段树的结构 ( 从 0 开始, 8 个元素 ) :

我们很容易得到建树的步骤, 这个步骤是递归定义的:

1. 如果当前区间只剩一个元素, 将维护的数据 ( 区间最值, 区间和 ) 赋值为序列中这一位置的数据
2. 否则取当前区间的中点, 将区间分为两部分, 对每一部分分别递归执行步骤 1 到 2
3. 两部分分别递归完成后, 将两部分的数据合并为当前区间的数据

区间查询操作步骤如下:

1. 如果当前区间被包含在目标区间内, 那么我们可以判定, 这是在之前递归时分出来的部分, 直接查询即可
2. 如果不是步骤 1 中的情况, 取当前区间的中点, 用二分搜索的方式, 将区间分为两部分, 接下来分为三种情况:
   1. 目标区间是当前区间的左半部分的一部分
   2. 目标区间是当前区间的右半部分的一部分
   3. 目标区间是当前区间的一部分 ( 即同时是左右两个部分的一部分 )
3. 按照这三种情况 ( 事实上写成代码就只有两个分支了, 1 和 3 与 2 和 3 可以分别合并而并没有冲突 ) 分别处理, 进行递归, 直到出现步骤 1 中的情况

当然, 线段树也支持单点查询和修改, 步骤如下:

1. 如果当前区间长度为 1 ( 左右端点相等 ) , 二分搜索过程保证了该区间仅包含目标点, 直接查询或修改
2. 如果不是步骤 1 中的情况, 则类似区间查询和修改, 不断二分当前区间, 此时没有上述的第三种情况, 其余相同, 进行递归即可

线段树是一棵完全二叉树, 则其深度为, 上述所有基本操作的时间复杂度都是二分搜索的

但是, 目前来看, 线段树的区间修改时间复杂度仍然不够优, 如果每次都用单点代替区间修改, 那么时间复杂度为, 不够快, 而如果使用类似区间查询的方式, 我们只会修改到最表层的 ( 即将原序列最优分割成的 ) 一层节点, 如果查询这些节点的子节点, 就会出现问题

这时我们可以采用一种经典的技巧: 懒标记

当修改操作发生时, 我们只修改最表层的节点, 并在这些节点上记录修改的内容, 这些内容可以叠加 ( 如一次 +5 的修改和一次 -5 的修改可以抵消, 一次 +5 的修改和一次 +3 的修改会变成一次 +8 的修改 ) , 在查询这些区间子节点操作发生前, 我们就让修改停留在这里, 因为没有影响

当查询操作发生时, 在向下递归的过程中, 如果遇到有懒标记的节点, 那么它的子节点一定还没有真正进行修改, 那我们只需要对其进行修改即可

同样地, 如果某个还未真正修改的节点是某次修改的最表层节点, 我们也要对其进行修改

因此考虑到对未真正修改节点进行修改的操作可以独立出来作为一个操作, 一般称作下传懒标记

代码实现

以下以支持查询区间和, 区间加为例

首先实现把子节点数据合并为父亲节点数据的函数 push_up, 以及下传懒标记的函数 push_down , 定义 tree 表示区间和, tag 表示懒标记:

void push_up(int current)  // 合并数据
{
    tree[current] = tree[current << 1] + tree[current << 1 | 1];  // 因为右移后最后一位必定是 0 , 故或 1 相当于加 1
}

void push_down(int from, int to, int current)  // 下传懒标记
{
    if (tag[current] && from != to)  // 叶子节点和无懒标记的节点不需要下传
    {
        tree[current << 1] += tag[current] * (middle - from + 1);
        tree[current << 1 | 1] += tag[current] * (to - middle);
        tag[current << 1] += tag[current];
        tag[current << 1 | 1] += tag[current];
        tag[current] = 0;
    }
}

然后我们可以实现建树, 令 a 表示原序列:

void build(int from, int to, int current)
{
    if (from == to)
    {
        tree[current] = a[from];
        return ;
    }

    int middle = (from + to) >> 1; 

    build(from, middle, current << 1);
    build(middle + 1, to, current << 1 | 1);  // 防止区间重叠
    push_up(current);
}

区间查询和区间修改如下:

int query(int left, int right, int from, int to, int current)
{
    if (left <= from && right >= to)  { return tree[current]; }

    int middle = (from + to) >> 1, answer = 0;

    push_down(from, to, current);
    if (left <= middle)  { answer += query(left, right, from, middle, current << 1); }
    if (middle < right)  { answer += query(left, right, middle + 1, to, current << 1 | 1); }

    return answer; 
}

void modify(int left, int right, int from, int to, int current, int modifier)
{
    if (left <= from && right >= to)
    {
        tree[current] += (to - from + 1) * modifier;
        tag[current] += modifier;

        return ;
    }

    int middle = (from + to) >> 1;

    push_down(from, to, current);
    if (left <= middle)  { modify(left, right, from, middle, current << 1, modifier); }
    if (middle < right)  { modify(left, right, middle + 1, to, current << 1 | 1, modifier); }
    push_up(current);
}

常用拓展

线段树的功能非常强大, 因而成为了使用最广泛的一种数据结构, 但目前还没有人系统阐述和整理线段树能够做的常用操作, 以使选手将题目 ( 变形后 ) 的要求迅速地和线段树联系起来; 由于本人水平有限, 刚刚入门数据结构, 这一总结可能并不全面

在简介和一些理解中所述的“线性可分”的说法上更进一步, 一般地而不形式化地, 线段树能够维护的数据必须支持如代码实现中所说的 push_down 和 push_up 两个操作, 即必须支持下传懒标记和合并数据两个操作

我们容易发现, 修改操作的类型一般与下传懒标记的实现有关, 而查询操作的类型一般与合并数据的实现有关; 以下所举的的操作的例子仅给出 push_down 和 push_up 实现

数学相关操作

区间和, 区间积与区间最值这六种操作与上面本质相同, 不在此赘述

区间开方理论上来说并不能用线段树维护 ( 理论上任何数据结构都无法维护 ) , 但是注意到开方是一个增长率绝对值很大的运算, 比如, 因此我们可以存储区间和并暴力开方, 当开方的区间的区间和小于其长度, 就不必再开方

区间三角函数相关的查询可做, 当且仅当修改操作是赋值或加法, 赋值是显然的, 对于加法, 我们想到:

即可维护

当然, 维护三角函数是一种很不常见的操作, 不过它启发我们, 抽象地说, 对于一种运算, 使得可用和表示, 那么以为修改的查询就是可做的

最大子段和

这是线段树一个很著名的应用, 例题如 SP1716 Can you answer these queries III ( GSS 中的一道题, GSS 的所有题都是数据结构好题, 推荐一做 ) , 只不过这题是单点修改

从题目中就可以看出, 这一应用与修改并没有太大的关系, 难点在于要维护哪些信息和如何正确合并两个子节点

首先, 我们肯定要存储最大子段和, 考虑这个最大值在哪两个端点取到:

1. 若两个端点在同一个子节点, 则取最值即可
2. 否则这一段必跨过两个子节点维护的区间, 那么此时最大子段和应为两个区间相交界处的最大子段和相加

综上所述, 这两个端点并不需要被存储也可以合并, 可以将这两个端点转化为两个更有用的数据, 即左起的最大子段和和右起的最大子段和, 这两个数据维护的方式与整体类似, 以左起为例:

1. 若两个端点都在左子节点, 赋值即可
2. 否则这一段必定包含整个左子节点和右子节点的左起一部分, 相加

一般在复杂的合并数据中, 我们常常定义一个 Node 结构体, 并重载它的加法运算符, 这样能使代码更加精简

示例代码如下, data 是维护的最大子段和, sum 是区间和:

struct Node
{
    int sum, data, left, right;
};

Node operator+(Node self, Node other)
{
    Node result = {  };

    result.sum = self.sum + other.sum;
    result.left = max(self.left, self.sum + other.left);
    result.right = max(other.right, other.sum + self.right);
    result.data = max(max(self.data, other.data), self.right + other.left);

    return result;
}

这种维护左起和右起的思想还可以进一步扩展, 如一道毒瘤题目 CF1731F Raging Thunder, 简要题意是:

给定一个字符串仅包含 > 和 < , 要求查询字符串中最长的一段连续子串, 满足前半段全为 > , 后半段全为 < , 并支持区间翻转操作

仿照上面的思想, 我们考虑存储左右两端最长的由同一种字符组成的连续子串的长度和类型, 当然, 也必须存储要查询的这个数据, 但这样我们就有了一个问题: 只存储最左和最右, 我们无法很好的处理子节点的合并

比如 <<<>>< 合并 <<><>< 得到 <<<>><<<><><, 理论上中间会产生一块 >><<< 这样的东西, 但是注意到 >> 这一块并未被存储, 因此还要维护两个额外信息: 第二左和第二右, 它们的类型可由最左最右推得

为了方便, 我们还需要维护子节点维护的子串的总长度; 为了翻转, 我们还需要顺便维护最长的一段连续子串, 满足后半段全为 > , 前半段全为 < , 这样翻转后, 它和我们要维护的数据就会交换

分类讨论思路:

1. 类型是否相同
2. 是否只有一段或只有两段
3. 是否覆盖一整个子节点 ( 尤其是维护 length_01 和 length_10 时 )

具体实现如下 ( 以布尔值 0 代表 > , 1 代表 < ) :

struct node
{
    bool l_color, r_color, tag;
    int length,
        l1, l2, r1, r2,
        length_01, length_10;
};

node operator+(node self, node other)
{
    node answer = {  };

    answer.length = self.length + other.length;
    answer.l_color = self.l_color;
    answer.r_color = other.r_color;

    if (self.l1 == self.length && self.l_color == other.l_color)  { answer.l1 = self.l1 + other.l1; }
    else  { answer.l1 = self.l1; }

    if (self.l1 + self.l2 == self.length && (self.r_color == other.l_color || !self.l2))
    {
        if (self.l1 == self.length && self.l_color == other.l_color)  { answer.l2 = self.l2 + other.l2; }
        else  { answer.l2 = self.l2 + other.l1; }
    }
    else  { answer.l2 = self.l2; }

    if (other.r1 == other.length && self.r_color == other.r_color)  { answer.r1 = self.r1 + other.r1; }
    else  { answer.r1 = other.r1; }

    if (other.r1 + other.r2 == other.length && (self.r_color == other.l_color || !other.r2))
    {
        if (other.r1 == other.length && self.r_color == other.r_color)  { answer.r2 = self.r2 + other.r2; }
        else  { answer.r2 = self.r1 + other.r2; }
    }
    else  { answer.r2 = other.r2; }

    answer.length_01 = max(self.length_01, other.length_01);
    answer.length_10 = max(self.length_10, other.length_10);
    if (self.r_color == other.l_color)
    {
        if (!self.r_color)
        {
            answer.length_01 = max(answer.length_01, self.r1 + other.l1 + other.l2);
            answer.length_10 = max(answer.length_10, self.r2 + self.r1 + other.l1);
        }
        else
        {
            answer.length_01 = max(answer.length_01, self.r2 + self.r1 + other.l1);
            answer.length_10 = max(answer.length_10, self.r1 + other.l1 + other.l2);
        }
    }
    else
    {
        if (!self.r_color)  { answer.length_01 = max(answer.length_01, self.r1 + other.l1); }
        else  { answer.length_10 = max(answer.length_10, self.r1 + other.l1); }
    }

    return answer;
}

node operator-(node self)
{
    swap(self.length_01, self.length_10);
    self.l_color ^= 1;
    self.r_color ^= 1;

    return self;
}

其中第二个重载运算符是一元减, 即负号, 代表翻转操作

区间数数

众所周知, 桶是一种值域和定义域互换的数据结构, 正常的数据结构维护位置 i 上有数据 x , 而桶维护数据等于 x 有哪些位置 ( 或者干脆只维护有几个 ) , 桶的常见应用是静态区间数数和桶排序, 桶的复杂度显然是的

注意到桶是一种线性的结构, 因而可以上线段树维护, 这就是权值线段树

权值线段树可以代替一般的平衡树 ( 对于不知道什么是平衡树的读者: 可以大致理解为一种在对数时间内, 动态维护一个集合和集合的偏序关系, 包括前驱, 后继, 整体第 k 大, 整体排名 ):

1. 插入和删除操作转化为单点修改
2. 查询第 k 大和查询排名转化为单点查询
3. 查询前驱和后继转化为查询排名再查询第 k 大, 一个小细节是, 查询的数可能不在集合里, 所以后继要特殊处理, 具体见代码

单点修改是不需要加懒标记的, 具体实现比较像在序列上二分, 比线段树模版还好写, 但是一般值域会很大, 需离散化

以 P3369 普通平衡树为例, 具体实现如下:

#include <iostream>
#include <map>
#include <algorithm>

using namespace std;

pair<int, int> queries[100001];
map<int, int> to_order, to_num;
int q, pointer, all[100001], tree[400001];

void push_up(int current);
int query_rank(int target, int from, int to, int current);
int query_num(int target, int from, int to, int current);
void modify(int target, int from, int to, int current, int modifier);

int main()
{
    cin >> q;
    for (int i = 1; i <= q; i++)
    {
        cin >> queries[i].first >> queries[i].second;
        if (queries[i].first != 4)  { all[++pointer] = queries[i].second; }
    }
    // 以下 6 行是离散化
    sort(all + 1, all + pointer + 1);
    for (int i = 1; i <= pointer; i++)
    {
        to_order[all[i]] = i;
        to_num[i] = all[i];
    }
    for (int i = 1; i <= q; i++)
    {
        int type = queries[i].first, x = queries[i].second, temp;

        if (type == 1)  { modify(to_order[x], 1, pointer, 1, 1); }
        else if (type == 2)  { modify(to_order[x], 1, pointer, 1, -1); }
        else if (type == 3)  { cout << query_rank(to_order[x], 1, pointer, 1) << endl; }
        else if (type == 4)
        {
            temp = query_num(x, 1, pointer, 1);
            cout << to_num[temp] << endl;
        }
        else if (type == 5)
        {
            temp = query_num(query_rank(to_order[x], 1, pointer, 1) - 1, 1, pointer, 1);
            cout << to_num[temp] << endl;
        }
        else
        {
            // query_rank 返回的是如果将 target 这个数插入集合, 它的排名
            // 查询后继时, 因为查询的数可能不在集合里, 所以会把后继向后顶一位, 使其排名比实际高, 因此不再加 1
            // 当然, 后继的定义是严格大于查询的数, 所以查询的数要加 1
            temp = query_num(query_rank(to_order[x] + 1, 1, pointer, 1), 1, pointer, 1);
            cout << to_num[temp] << endl;
        }
    }

    return 0;
}

void push_up(int current)
{
    tree[current] = tree[current << 1] + tree[current << 1 | 1];
}

int query_rank(int target, int from, int to, int current)
{
    if (from == to)  { return 1; }

    int middle = (from + to) >> 1;

    if (target <= middle)  { return query_rank(target, from, middle, current << 1); }
    else  { return tree[current << 1] + query_rank(target, middle + 1, to, current << 1 | 1); }
}

int query_num(int target, int from, int to, int current)
{
    if (from == to)  { return from; }

    int middle = (from + to) >> 1;

    if (tree[current << 1] >= target)  { return query_num(target, from, middle, current << 1); }
    else  { return query_num(target - tree[current << 1], middle + 1, to, current << 1 | 1); }
}

void modify(int target, int from, int to, int current, int modifier)
{
    if (from == to)
    {
        tree[current] += modifier;
        return ;
    }

    int middle = (from + to) >> 1;

    if (target <= middle)  { modify(target, from, middle, current << 1, modifier); }
    else  { modify(target, middle + 1, to, current << 1 | 1, modifier); }
    push_up(current);
}

二维偏序

上述的权值线段树的另一个常见应用, 也常常使用类似的权值树状数组

二维偏序的形式化描述如下: 对于两种可以相同的偏序关系和, 给定点对求出所有满足且的点对的点对的数量

而偏序可以理解成一种广义的大小关系, 对于数和, 偏序和和的真值是唯一确定的, 而且其中只有一种为真

对于题目 P1908 逆序对, 这道题的要求等价于, 将每一个数转化为点对, 偏序关系分别是大于和小于, 即可

二维偏序的统一做法是, 离线, 先按其中一维排序, 然后将另一维的值插入到权值线段树中, 查询前缀和即可

具体实现是容易的, 这里略去

常用扩展

动态开点线段树

由于线段树的结构是一颗完全二叉树, 因而它最多浪费 4 倍的空间, 但是有些题目的树结构很 “稀疏” , 如果这时还开满, 就太浪费空间了

事实上, 我们可以只建需要的节点, 将原本处于 和 的左右节点, 连续地开到当前最后一个节点的索引后, 然后在节点维护的信息中, 将其加入, 这样数据就连续了

与普通线段树没有什么太大区别, 而且主要应用于可持久化中, 示例代码暂不给出

标记永久化

可持久化需要的另一个技巧是标记永久化, 即懒标记不下传, 每次询问, 自上而下累计路径上的所有懒标记即可, 虽说亦没有太大区别, 但因为技巧比较抽象, 我就不太能看文字实现出来, 所以还是有这样一份能过模版的代码 ( 没有区别的地方略去 ) :

int query(int left, int right, int from, int to, int current)
{
    if (left <= from && right >= to)  { return tree[current] + (to - from + 1) * modifier; }

    int middle = (from + to) >> 1, answer = 0;

       answer += (min(right, to) - max(left, from) + 1) * modifier;
    if (left <= middle)  { answer += query(left, right, from, middle, current << 1); }
    if (middle < right)  { answer += query(left, right, middle + 1, to, current << 1 | 1); }

    return answer; 
}

void modify(int left, int right, int from, int to, int current, int modifier)
{
    if (left <= from && right >= to)
    {
        tag[current] += modifier;
        return ;
    }

    int middle = (from + to) >> 1;

    tree[current] += (min(right, to) - max(left, from) + 1) * modifier;
    if (left <= middle)  { modify(left, right, from, middle, current << 1, modifier); }
    if (middle < right)  { modify(left, right, middle + 1, to, current << 1 | 1, modifier); }
    push_up(current);
}

为什么数据合并不能省去? 因为这不但要求自下而上查询, 而且要求这一条查询的路径刚好经过每一个还未被修改的, 数据暂时是错误的点, 这种操作难以在不改变复杂度的情况下实现

zkw 线段树

当我们将线段树的实现倒转, 自下而上, 从叶子遍历至根节点, 就得到了 zkw 线段树, 它使用循环实现, 加以位运算优化, 常数很小, 代码量也有显著优势

在普通线段树中, 我们使用递归, 目的是为了定位叶子节点, 不使用循环, 是因为无法确定叶子的深度; 而一旦我们从叶子出发, 则没有必要了

为了方便定位叶子的位置, 我们强行将线段树开成满二叉树, 深度统一, 当然, 多出来的节点不用就可以了; 除此之外, 它的存储结构和普通线段树并没有区别

由于不使用递归, 懒标记下传很难实现, 因此我们强制标记永久化

以下是一些树结构和位运算的前置知识:

1. 设代表一个非根节点 ( 的索引, 下同 ) , 若其为父亲的右子节点, 则是奇数, 其兄弟节点显然是, 类似地, 若其为父亲的左子节点, 则是偶数, 兄弟节点为为, 为了避免分类讨论, 以位运算代表; 类似地, 若节点和, 若, 则它们互为兄弟节点, 则是不互为兄弟节点
2. i << 1 和 i << 1 | 1 分别代表乘 2 和乘 2 加 1 , 与普通线段树一样, 用于求得左右子节点
3. 设代表一个非根节点, 其父亲为
4. 在满二叉树中, 最后一层叶子节点的数量严格比上面所有节点数量多 1 , 因此最后一层叶子节点的数量是, 其中显然是原序列长度; 总节点数是; 树的高度是
5. 对于原序列上一个索引, 它在最后一层叶子节点中一定有对应, 这个对应的节点, 在树中的索引应该, 是

下面的具体实现仍以支持查询区间和, 区间加为例

区间然后我们从建树开始, 这次可以直接将原序列赋值到对应的叶子节点了, 之后只需要将非叶子节点从两个已合并的节点合并过来即可, 注意合并顺序:

void build()
{
    leaves = 1 << int(ceil(log2(n)));
    for (int i = 1; i <= n; i++)  { tree[i + leaves] = a[i]; }
    for (int i = leaves; i >= 1; i--)  { tree[i] = tree[i << 1] + tree[i << 1 | 1]; }
}

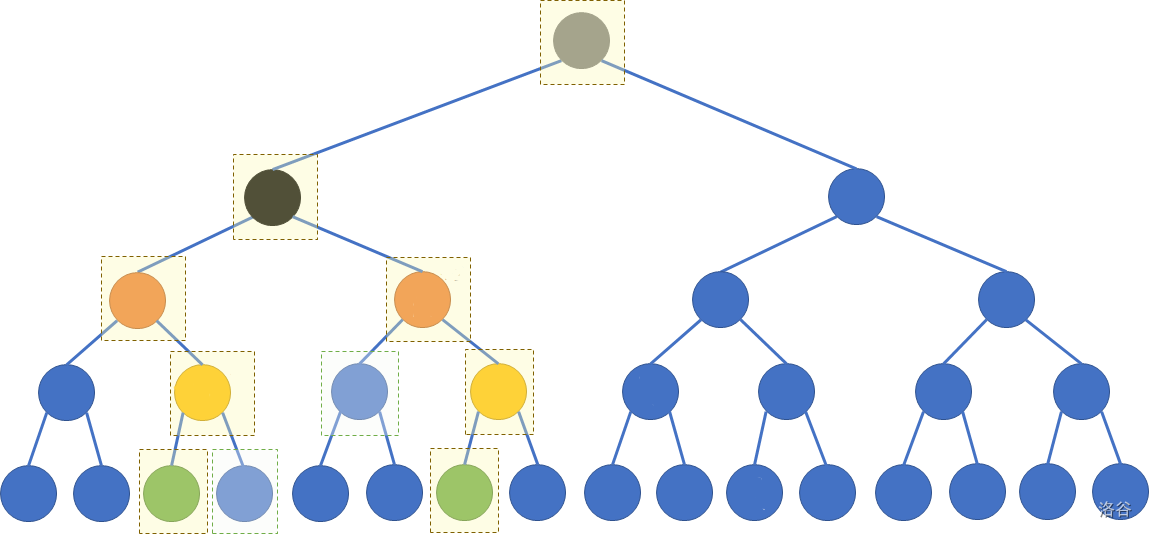
接下来是区间查询, 考虑将询问变成开区间, 那么从询问的两个端点向上遍历到根, 这两条路径中间 “夹着的” 就是我们要查询的数据, 但因为线段树的每一层实际都维护了原序列, 因此每一区间的数据仅在第一次出现时被合并入答案

何时第一次出现呢? 考虑在 “夹着的” 区间内, 与路径紧挨的那些节点, 当它们与路径中某个节点是兄弟节点时, 它就是第一次出现; 如图, 黄色虚线框代表两条路径, 绿色虚线框代表第一次出现的节点

实现上, 我们需要特判黑色节点这一段, 否则会重复合并

代码实现如下:

int query(int left, int right)
{
    // 由于线段树每一层的子节点维护的区间长度是相同的, 以 length 代表当前层的区间长度
    // l_length 为 left 所在区间的长度, r_length 同理
    int result = 0, length = 1, l_length = 0, r_length = 0;

    left += leaves - 1;
    right += leaves + 1;
    for ( ; left ^ right ^ 1; left >>= 1, right >>= 1, length <<= 1)
    {
        result += l_length * tags[left] + r_length * tags[right];  // 标记永久化
        if (~left & 1)  // 位运算判断 left 是否是奇数, 以判断是否是左子节点
        {
            result += tree[left ^ 1];
            l_length += length;
        }
        if (right & 1)  // 同上, 判断是否是右子节点
        {
            result += tree[right ^ 1];
            r_length += length;
        }
    }
    for ( ; left; left >>= 1, right >>= 1)  { result += l_length * tags[left] + r_length * tags[right]; }  // 特判到根的一段

    return result;
}

自然, 区间修改是很类似的:

void modify(int left, int right, int modifier)
{
    int length = 1, l_length = 0, r_length = 0;

    left += leaves - 1;
    right += leaves + 1;
    for ( ; left ^ right ^ 1; left >>= 1, right >>= 1, length <<= 1)
    {
        tree[left] += l_length * modifier;
        tree[right] += r_length * modifier;
        if (~left & 1)
        {
            tree[left ^ 1] += length * modifier;
            tags[left ^ 1] += modifier;
            l_length += length;
        }
        if (right & 1)
        {
            tree[right ^ 1] += length * modifier;
            tags[right ^ 1] += modifier;
            r_length += length;
        }
    }
    for ( ; left; left >>= 1, right >>= 1)
    {
        tree[left] += l_length * modifier;
        tree[right] += r_length * modifier;
    }
}

关于树状数组

关于树状数组有一种有趣的认识, 来自于 Alex_Wei 大佬, 即树状数组是舍弃了右子节点的线段树, 因而其查询区间的一侧变成了开区间, 只能维护像前缀和这样具有可减性的数据, 也因此常数缩短了约 8 到 10 倍

我们接受这种想法, 因而不对树状数组再做过多介绍, 完备的模版如下:

int n, a[MAX_N], tree[MAX_N];

int lowbit(int x)
{
    return x & -x;
}

void build()  // 线性复杂度建树
{
    for (int i = 1; i <= n; i++)
    {
        int j = i + lowbit(i); 
        
        tree[i] += a[i];
        if (j <= n)  { tree[j] += tree[i]; }
    }
}

int query(int x)  // 从 1 到 x 的前缀和
{
    int result = 0;
    
    while (x)
    {
        result += tree[x];
        x -= lowbit(x);
    }
    
    return result;
}

void modify(int x, int y)  // 将位置 x 加上 y
{
    while (x <= n)
    {
        tree[x] += y;
        x += lowbit(x);
    }
}

当然, 由于树状数组存储的是前缀和, 线性建树也可以使用前缀和实现