1. 前言
2. 引入
3. 文字实现
4. 但什么是状压 DP
5. 代码实现

前言

状态压缩动态规划, 简称状压 DP , 是一种非常优雅的算法, 一般来说, 思维难度和实现难度都不高, 概念也比较容易理解, 同时非常有特点, 易于辨认, 洛谷蓝题以下的状压 DP 都相当好写

但是状压 DP 的定义不是我想探究的, 事实上, 我试图通过一道相当巧妙的题目, 即 P2150 寿司晚宴, 来重新叙述一道困难的状压 DP 从无到有的完整思考过程

引入

首先读题, 并对题面进行形式化, 形式化题面如下:

维护两个集合和, 使得:

1. ,
2. ,
3. , ,

请你求出所有可能的方案数对取模的结果

从题面中可以得到, 本题需要维护集合, 这是状压 DP 的典型特征之一

然后观察数据范围, 非常小, 但是没有小到可以直接状态压缩的程度 ( 是不可能开下的 )

那么此时, 我们再次阅读题面, 找出题面中最特殊的部分, 对于此题, 应该是形式化题面的第三条, 互质

互质说明两个数没有任何相同的因数, 注意到, 因数时常表示为集合, 事实上我们仍在维护集合, 那么考虑对于因数集合进行状态压缩:

对于任意正整数, 显然不可能同时存在两个大于的质因数, 注意到, 这个数据范围就可以状态压缩了, 剩下的那个大质因数单独处理即可

综上, 我们确定了此题可以进行状压 DP, 依据是: 维护集合, 数据范围可压缩

文字实现

阅读以下文字时, 请时刻确保你理解: 我们虽然选择的是数, 但维护的是小质因数集; 集合和维护的是数, 而不是小质因数集

我们知道, 小于等于 22 的数中, 只有 8 个质数, 用一个二进制串表示, 如果这一部分互质, 我们称其为弱互质

多出来的这一个大质因数有很多种可能 ( 也可能没有 ) , 如果两个状态是弱互质的, 且它们的大质因数不相同, 那么这两个状态是互质的, 如果两个数的大质因数相同, 那么无论如何这两个状态都不可能互质

因此我们需要采用类似离散化去重的方式, 将大质因数排序, 这样大质因数就分为了若干段, 每段内是相等的, 这样, 可以分类讨论, 即该大质因数属于集合和该大质因数属于集合, 显然不可能同时属于两个集合

分类讨论决定了我们需要两个 DP 数组, 但是, 每段的大质因数不同, 因此该 DP 数组实际上是局部的, 即只生效于此段内部, 这是显然的, 那么我们还需要一个全局的数组来存储最终的答案

定义表示集合此时所有被选的数的小质因数集的并 ( 的二进制表示, 下同 ) 是, 不被选的并是, 在此大质因数段此种情况下的方案数

定义表示集合此时所有被选的数的小质因数集的并是, 不被选的并是, 在此大质因数段此种情况下的方案数

注意, 以上两个数组是互斥的, 再次强调: 如果两个数的大质因数相同, 那么无论如何这两个状态都不可能互质 ( 但在一种情况下不互斥, 请读者在阅读到下方答案前尝试自己思考是何时 )

定义表示集合所有被选的数的小质因数集的并是, 集合所有被选的数的小质因数集的并是, 在此种情况下的方案数

问题来了, 如何把两个局部数组的值合并到全局数组呢?

首先, 从两个局部数组的角度来说, 之前的决策和结果对它们是封闭的且有影响的, 所以, 为了提供足够的信息, 我们需要先 “告诉” 它们这些东西, 即将全局数组复制到两个数组中

我们不能直接加上这两个数组的值, 因为有重复的贡献

我们可以考虑赋值, 但这样仍有一部分重复贡献, 不过这是可以消除的: 设若该段内没有任何数被选择, 那么两个数组都含有此种情况, 此时不互斥; 根据定义, 全局数组此时的值就是该段内没有任何数被选择的方案数 ( 为什么? 因为它相当于还未进入此段 )

综上, 合并所用的状态转移方程如下:

这部分极难理解, 理解完成后剩余部分相当轻松愉快, 如还未理解可结合下面示意图理解 ( 代表第个大质因数 ):

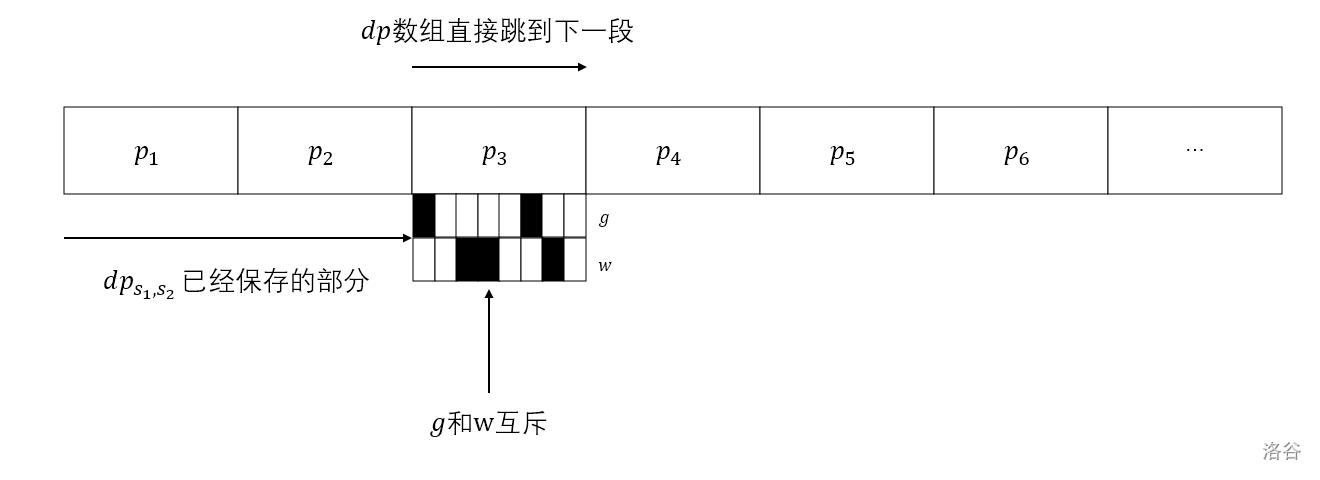
总的步骤如下:

1. 预处理中的所有整数的小质因数二进制表示和大质因数, 并根据大质因数排序
2. 遍历所有的大质因数段, 注意没有大质因数的也算一段
3. 对于每一段, 按如下操作:
   1. 清空局部 DP 数组
   2. 遍历所有可能的和, 进行状态转移, 令表示的质因数集, 状态转移方程如下:
      
4. 合并状态

但什么是状压 DP

如果你不知道什么是状压 DP , 那么考虑按照线性 DP 的思路来定义状态:

1. 首先, 你不能存两人各选了多少, 因为这样显然无法转移
2. 然后, 你不能存两人各自最后选了什么, 因为前面的也要考虑
3. 那么, 最后你会发现, 你需要存两人各自选了什么, 但是这样 DP 的维数不确定
4. 于是想到使用标记数组标记, 对于两个人而言, 哪些选过, 哪些没选过
5. 然而标记数组无法塞进 DP 数组的维度中, 因此我们可以想到用 map 存储, 这是一种解决方案
6. 但主流的解决方案是, 将标记数组视作一个二进制串, 将二进制串视为整数, 塞进 DP 数组中

这就是状压 DP

代码实现

代码比较难写, 首先写出取模的代码, 如下:

ll modding(ll num)
{
    return num < mod ? num : num - mod;
}

不要使用常规取模, 因为在状态转移过程中可能存在负数

然后是预处理小质因数集和大质因数段, 代码如下:

const vector<int> primes = { 2, 3, 5, 7, 11, 13, 17, 19 };

pair<int, int> mark(int num)
{
    int marker = 0, index = 0;

    for (auto prime : primes)
    {
        while (!(num % prime))  // 质因数分解
        {
            num /= prime;
            marker |= 1 << index;
        }
        index++;
    }

    return { num, marker };  // 质因数分解剩下的就是大质因数
}

在主函数内加入:

for (int i = 2; i <= n; i++)  { markers[i] = mark(i); }
sort(markers + 2, markers + n + 1);  // 按照大质因数排序

接下来是 DP 部分:

for (int i = 2; i <= n; i++)
{
    if (markers[i].first == 1 || markers[i].first != markers[i - 1].first)  // 判断是否进入了一个新段
    {
        for (int pattern1 = (1 << 8) - 1; pattern1 >= 0; pattern1--)
        {
            for (int pattern2 = (1 << 8) - 1; pattern2 >= 0; pattern2--)
            {
                if (pattern1 & pattern2)  { continue; }  // 两个数组互斥

                dp[pattern1][pattern2] = modding(mod - dp[pattern1][pattern2] + modding(dp1[pattern1][pattern2] + dp2[pattern1][pattern2]));  // 合并到全局数组

                // 在一个循环中同时完成合并和复制
                dp1[pattern1][pattern2] = dp[pattern1][pattern2];
                dp2[pattern1][pattern2] = dp[pattern1][pattern2];
            }
        }
    }

    int marker = markers[i].second;

    for (int pattern1 = (1 << 8) - 1; pattern1 >= 0; pattern1--)
    {
        for (int pattern2 = (1 << 8) - 1; pattern2 >= 0; pattern2--)
        {
            if (pattern1 & pattern2)  { continue; }

            if (!(pattern2 & marker))  { dp1[pattern1 | marker][pattern2] = modding(dp1[pattern1 | marker][pattern2] + dp1[pattern1][pattern2]); }
            if (!(pattern1 & marker))  { dp2[pattern1][pattern2 | marker] = modding(dp2[pattern1][pattern2 | marker] + dp2[pattern1][pattern2]); }
        }
    }
}

for (int pattern1 = (1 << 8) - 1; pattern1 >= 0; pattern1--)
{
    for (int pattern2 = (1 << 8) - 1; pattern2 >= 0; pattern2--)
    {
        if (pattern1 & pattern2)  { continue; }

        dp[pattern1][pattern2] = modding(mod - dp[pattern1][pattern2] + modding(dp1[pattern1][pattern2] + dp2[pattern1][pattern2]));

        answer += dp[pattern1][pattern2];
        answer %= mod;
    }
}

cout << answer << endl;